2021CSP-J组初赛真题解析22-43

真题解析22

22. 输出的第二行一定是由小写字母、大写字母、数字和“+”、“/”、“=”构成的字符串。（  ）

注：22-24题为阅读程序题型中的判断题,25-27题为阅读程序题型中的选择题。

解析：

背景知识：

ASCII编码：（American Standard Code for Information Interchange）美国国家信息交换标准字符码。用7个二进制数表示1个字符的字符编码。ASCII一共可以表示128种不同的字符。用户使用计算机时，从标准输入设备键盘输入的各种字符，由计算机自动转换后，以ASCII码的形式输入到计算机中。

Base64编码： Base64是一种编码方式，这个术语最初是在“MIME内容传输编码规范”中提出的。Base64不是一种加密算法，它实际上是一种“二进制转换到文本”的编码方式，它能够将任意二进制数据转换为ASCII字符串的形式，以便在只支持文本的环境中也能够顺利地传输二进制数据。

base64编码：把二进制数据转为字符

base64解码：把字符转为二进制数据

知识点分类：

数学-数及其运算-编码

答案解析：

首先分析下题目所给的代码：

base数组：

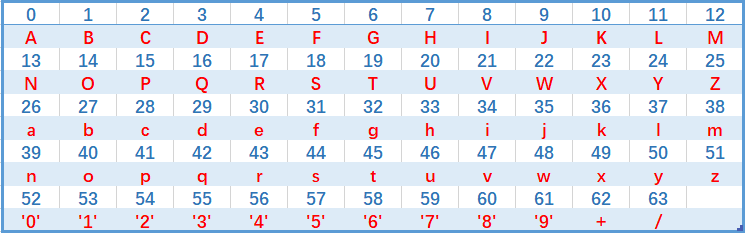
base数组的下标值对应为0~63，对应字符（ASCII码）A-Z,a-z,’0′-‘9’,+,/。

table数组：

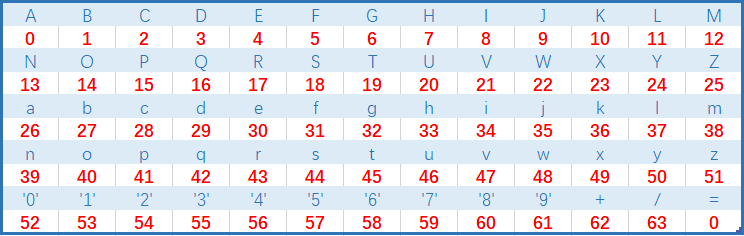
table数组的下标值对应为字符（ASCII码）A-Z,a-z,’0′-‘9’,+,/ 对应0~63，字符（ASCII码）= 也对应0。

table数组的下标范围是字符A-Z,a-z,0-9,+，/,=，对应的值是0-63。根据代码分析，对0-63进行decode函数中的各种位运算，得到的结果不一定是A-Z,a-z,0-9,+，/,= 也有可能会出现空格等字符，例如下图程序运行结果中就出现了空格字符。

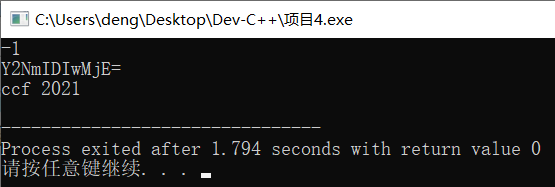
所以本题的描述是错误的，应该在括号内打×。

真题解析23

23. 可能存在输入不同，但输出的第二行相同的情形。（  ）

注：22-24题为阅读程序题型中的判断题,25-27题为阅读程序题型中的选择题。

解析：

背景知识：

ASCII编码：（American Standard Code for Information Interchange）美国国家信息交换标准字符码。用7个二进制数表示1个字符的字符编码。ASCII一共可以表示128种不同的字符。用户使用计算机时，从标准输入设备键盘输入的各种字符，由计算机自动转换后，以ASCII码的形式输入到计算机中。下图为十进制索引表示的ASCII码字符集：

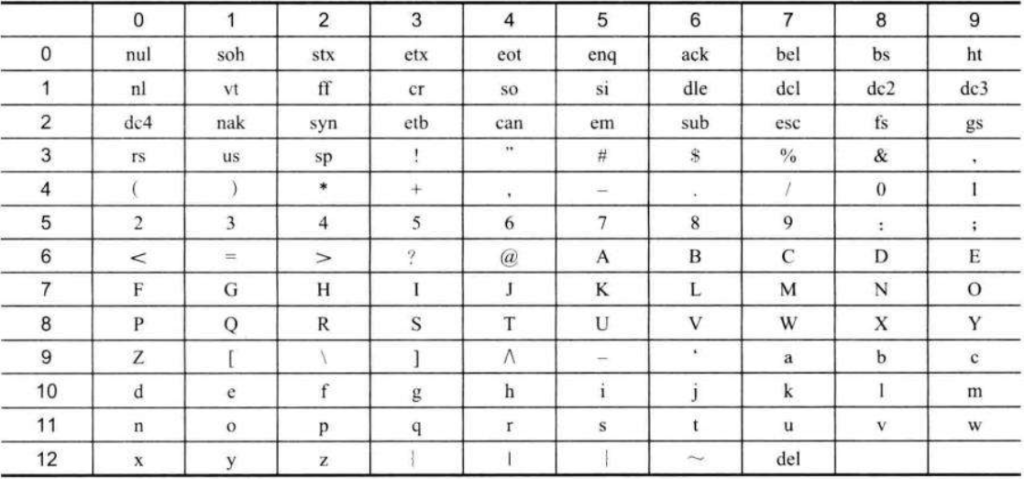
Base64编码： Base64是一种编码方式，这个术语最初是在“MIME内容传输编码规范”中提出的。Base64不是一种加密算法，它实际上是一种“二进制转换到文本”的编码方式，它能够将任意二进制数据转换为ASCII字符串的形式，以便在只支持文本的环境中也能够顺利地传输二进制数据。

base64编码：把二进制数据转为字符

base64解码：把字符转为二进制数据

知识点分类：

数学-数及其运算-编码

答案解析：

首先分析下题目所给的代码：

当输入b0==时：

table[b]=27

table[0]=52

table[=]=0

table[=]=0

输出的第一个字符：27<<2 | 52>>4 即00011011<<2 | 00110100>>4 = 111

根据背景知识中的ASCII码字符集可知111对应的字符是‘o’

输出的第二个字符：52<<2 | 0>>4 即00110100<<2 | 00000000>>4 = 208

超出了ASCII码字符集的范围，所以没有字符输出。

输出的第三个字符：0<<2 | 0>>4 即00000000<<2 | 00000000>>4 = 0

根据背景知识中的ASCII码字符集可知0对应的字符是空，所以没有字符输出。

也可以通过编译运行程序验证：

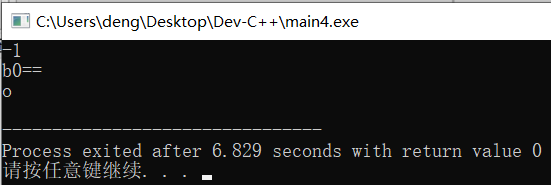
输入为b0==时，输出为小写字母o

---

当输入b1==时：

table[b]=27

table[1]=53

table[=]=0

table[=]=0

输出的第一个字符：27<<2 | 53>>4 即00011011<<2 | 00110101>>4 = 111

根据背景知识中的ASCII码字符集可知111对应的字符是‘o’

输出的第二个字符：53<<2 | 0>>4 即00110101<<2 | 00000000>>4 = 324

超出了ASCII码字符集的范围，所以没有字符输出。

输出的第三个字符：0<<2 | 0>>4 即00000000<<2 | 00000000>>4 = 0

根据背景知识中的ASCII码字符集可知0对应的字符是空，所以没有字符输出。

也可以通过编译运行程序验证：

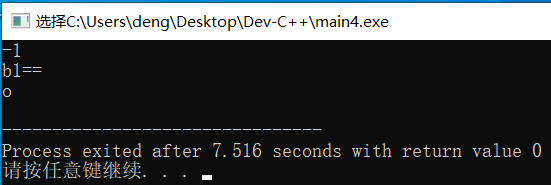
输入为b1==时，输出为小写字母o

---

上述例子中输入不同，但输出的第二行是相同的，所以本题的描述是正确的，应该在括号内打√。

真题解析24

24. 输出的第一行为“-1”。（   ）

注：22-24题为阅读程序题型中的判断题,25-27题为阅读程序题型中的选择题。

解析：

背景知识：

数在计算机中的表示：

机器数是将符号”数字化”的数，是数字在计算机中的二进制表示形式。机器数有2个特点：一是符号数字化，二是其数的大小受机器字长的限制。机器数分为无符号数和有符号数。

无符号数：所有的位全部用来表示数本身

有符号数：某些位用来表示数的符号，其他的位用来表示数值本身。

有符号数的整数的表示方式主要有：原码、反码、补码。计算机中所有数都是以补码形式存储的。

原码：

正数原码是转换成二进制后在前边加0

负数原码是转换成二进制后在前边加1

反码：

正数的反码是其本身

负数的反码是在其原码的基础上，符号位不变，其余各个位取反

补码：

正数的补码就是其本身

负数的补码是在其原码的基础上，符号位不变，其余各数取反，最后+1

知识点分类：

数学-数及其运算-编码

答案解析：

首先分析下题目所给的代码：

根据代码分析可知，对应输出第一行的代码为：
cout << int(table[0]) << end1;

table[0]=0xff。其中，0x表示这是一个十六进制的数;ff是这个十六进制数的数值，转换成二进制就是：11111111

根据背景知识中关于负数在计算机内存储的方式可知：11111111是-1的补码，所以int(0xff)=-1。

也可以通过编译运行程序验证：

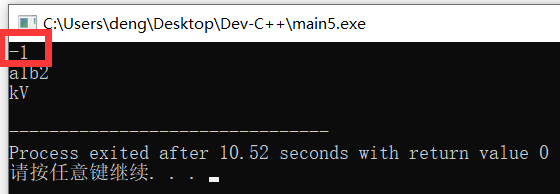
可以看出，第一行的输出为-1，所以本题的描述是正确的，应该在括号内打√。

真题解析25

题目代买如上：

25. 设输入字符串长度为n，decode函数的时间复杂度为（  ）。

A. θ(√n)

B. θ(n)

C. θ(nlogn)

D. θ(n^2)

注：22-24题为阅读程序题型中的判断题,25-27题为阅读程序题型中的选择题。

解析：

背景知识：

算法：描述求解问题方法的操作步骤集合。算法描述一般有三种形式：

1.文字形式：用中文或者英文等文字来描述算法

2.伪代码形式：用一种称为伪代码的类程序设计语言来描述算法

3.程序设计语言形式：用某种程序设计语言描述算法

算法时间复杂度：算法为了完成任务所需要的执行的基本运算的次数。

常见的算法时间复杂度有：

常数阶O(1)，对数阶O（log₂n）,线性阶O（n）等。

算法空间复杂度：执行算法所需要的的内存空间。

知识点分类：

算法-算法概念与描述-算法概念

答案解析：

首先分析下题目所给的代码：（如上）

根据对代码的分析可知，decode函数对字符串中的字符进行遍历，每次字符常数次操作，所以时间复杂度为O(字符串长度）= O（n）, 正确答案应该选择B。

真题解析26

26. 当输入为“Y3Nx”时，输出的第二行为（  ）。

A. “csp”

B. “csq”

C. “CSP”

D. “Csp”

解析：

背景知识：

ASCII编码：（American Standard Code for Information Interchange）美国国家信息交换标准字符码。用7个二进制数表示1个字符的字符编码。ASCII一共可以表示128种不同的字符。用户使用计算机时，从标准输入设备键盘输入的各种字符，由计算机自动转换后，以ASCII码的形式输入到计算机中。下图为十进制索引表示的ASCII码字符集：

base数组：

base数组的下标值对应为0~63，对应字符（ASCII码）A-Z,a-z,’0′-‘9’,+,/。

table数组：

table数组的下标值对应为字符（ASCII码）A-Z,a-z,’0′-‘9’,+,/ 对应0~63，字符（ASCII码）= 也对应0。

知识点分类：

数学-数及其运算-编码

答案解析：

首先分析下题目所给的代码：（如上）

当输入Y3Nx时,如下图所示：

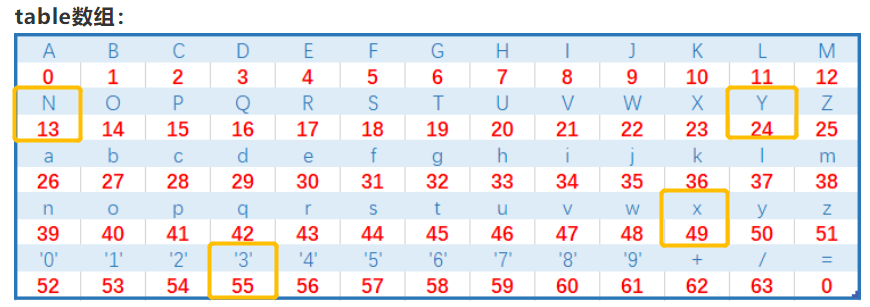
table[Y]=24

table[3]=55

table[N]=13

table[x]=49

输出的第一个字符：24<<2 | 55>>4 即00011000<<2 | 00110111>>4 = 99

根据背景知识中的ASCII码字符集可知99对应的字符是‘c’

输出的第二个字符：(55&0x0f)<<4 | 13>>2即

（00110111&00001111）<<4 | 00001101 >>2 =115

根据背景知识中的ASCII码字符集可知115对应的字符是‘s’

输出的第三个字符：13<<6 | 49 即00001101<<6 | 00110001 = 113

根据背景知识中的ASCII码字符集可知113对应的字符是‘q’

也可以通过编译运行程序验证：

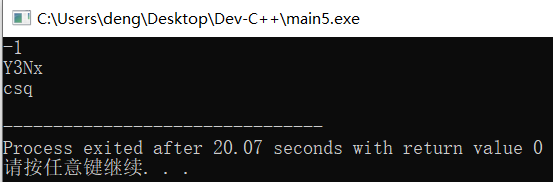
输入为Y3Nx时，输出为csq

---

可见当输入为“Y3Nx”时，输出的第二行为“csq”，正确答案应该选择B。

真题解析27

代码如上

27. 当输入为“Y2NmIDIwMjE=”时，输出的第二行为（  ）。

A. “ccf2021”

B. “ccf2022”

C. “ccf 2021”

D. “ccf 2022”

解析：

背景知识：

ASCII编码：（American Standard Code for Information Interchange）美国国家信息交换标准字符码。用7个二进制数表示1个字符的字符编码。ASCII一共可以表示128种不同的字符。用户使用计算机时，从标准输入设备键盘输入的各种字符，由计算机自动转换后，以ASCII码的形式输入到计算机中。

base数组：/table数组：（如上）

知识点分类：

数学-数及其运算-编码

答案解析：

首先分析下题目所给的代码：（如上）

本题如果按照26题的方法计算，虽然可以得出正确答案，但是花费的时间较长，计算量也较大。在考试中建议结合选项使用排除法进行计算。题目中的输入为：Y2NmIDIwMjE=。通过本题前几道小题的分析可以确定，输出应该为8位字符串，而且最后两个字符是不同的。

也可以通过编译运行程序验证：

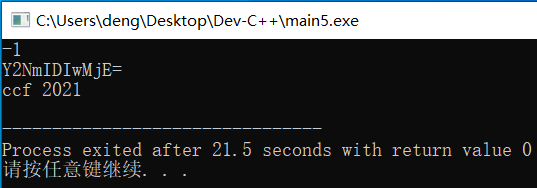
输入为Y2NmIDIwMjE=时，输出为ccf 2021

---

可见当输入为“Y2NmIDIwMjE=”时，输出的第二行为“ccf 2021”，正确答案应该选择C。

真题解析28

假设输入的x是不超过1000的自然数，完成下面的判断题和单选题：

28. 若输入不为”1″，把第12行删去不会影响输出的结果。（   ）

解析：

背景知识：

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

埃氏筛法：埃拉托斯特尼筛法，简称埃氏筛法。是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

知识点分类：

数学-初等数论-埃氏筛法和线性筛法求素数

答案解析：

首先分析下题目所给的代码：

通过对代码的分析可知，如果输入不为“1”，第13行的f[1]和g[1]就不会影响后续的程序运行。

也可以通过编译运行程序验证：

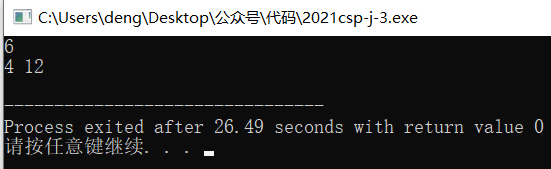
输入不为1，程序可以正常运行。

---

所以本题的描述是正确的，应该在括号内打√。

29. 第24行的” f[i]/c[i*k]”可能存在无法整除而向下取整的情况。（   ）

解析：

背景知识：

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

埃氏筛法：埃拉托斯特尼筛法，简称埃氏筛法。是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

知识点分类：

数学-初等数论-埃氏筛法和线性筛法求素数

答案解析：

首先分析下题目所给的代码：

根据代码分析可知：

f[i]表示整数i的质因数个数；

c[i*k]表示i*k的最小质因数个数；

f[i]=(1+number_1)(1+number_2)…(1+number_m)

c[i*k]=c[i] + 1 = number_1+ 1

这两个数一定是倍数关系。

所以本题的描述是错误的，应该在括号内打×。

30. 在执行完init()后，f数组不是单调递增的，但g数组是单调递增的。（   ）

解析：

背景知识：

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

埃氏筛法：埃拉托斯特尼筛法，简称埃氏筛法。是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

函数的单调性：函数的单调性也叫做函数的增减性。当函数的自变量在其定义区间内增大（或减小）时，函数值也随着增大（或减小），则称该函数为在该区间上具有单调性。

知识点分类：

数学-初等数论-埃氏筛法和线性筛法求素数

答案解析：

首先分析下题目所给的代码：（如上）

本题我们可以计算i取不同的值时，f数组和g数组值的变化情况来判断题干的描述是否正确：

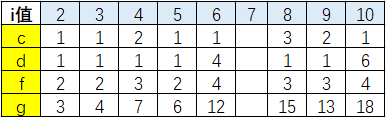
计算结果如上图所示。从上图的计算结果中我们可以看出，数组f和数组g的值都不是单调递增的，所以本题的描述是错误的，应该在括号内打×。

31. init函数的时间复杂度为（   ）。

A. θ(n)

B. θ(nlogn)

C. θ(n√n)

D. θ(n^2)

解析：

背景知识：

算法：描述求解问题方法的操作步骤集合。算法描述一般有三种形式：

1.文字形式：用中文或者英文等文字来描述算法

2.伪代码形式：用一种称为伪代码的类程序设计语言来描述算法

3.程序设计语言形式：用某种程序设计语言描述算法

算法时间复杂度：算法为了完成任务所需要的执行的基本运算的次数。

常见的算法时间复杂度有：

常数阶O(1)，对数阶O（log₂n）,线性阶O（n）等。

算法空间复杂度：执行算法所需要的的内存空间。

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

知识点分类：

算法-算法概念与描述-算法概念

答案解析：

首先分析下题目所给的代码：（如上）

从代码分析可以看出，依据合数=最小质因数 × 最大因数（非这个合数）这个等式，init函数让每个合数只被筛查了一次，但并不意味着程序只需要遍历一遍就可以完成素数的筛查，实际上每遍历到一个数就要有相应的操作，只是这些操作的复杂度很低，在N前可以忽略不计。所以init函数的时间复杂度接近于O(n)。

根据以上分析，本题的正确答案应该选择A。

32. 在执行完init()后，f[1], f[2], f[3] …… f[100]中有（    ）个等于2。

A. 23

B. 24

C. 25

D. 26

解析：

背景知识：

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

埃氏筛法：埃拉托斯特尼筛法，简称埃氏筛法。是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

知识点分类：

数学-初等数论-埃氏筛法和线性筛法求素数

答案解析：

首先分析下题目所给的代码：（如上）

通过对代码的分析可知，f[i]存放的是质数的个数，所以本题实际上就是求

1-100中有多少个质数。1-100中的质数如下（共25个）：

所以本题的正确答案应该选C。

33. 当输入”1000″时，输出为（  ）。

A. “15 1340”

B. “15 2340”

C. “16 2340”

D. “16 1340”

解析：

背景知识：

素数：素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

埃氏筛法：埃拉托斯特尼筛法，简称埃氏筛法。是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

欧拉筛法：欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。

知识点分类：

数学-初等数论-埃氏筛法和线性筛法求素数

答案解析：

首先分析下题目所给的代码：（如上）

本题是求数字1000的质因数个数和质因数的和。

因为：1000=10³ =（2*5）=2³*5³=(2⁰*2³)*(5⁰*5³)

第一个括号内有4种可能：

1，2，4，8

第二个括号内有4种可能：

1，5，25，125

^{所以数字1000的质因数个数是4*4=16}

^又因为：

2⁰*5⁰+2⁰*5¹+2⁰*5²+2⁰*5³=

2⁰*(5⁰+5¹+5²+5³)

2¹*5⁰+2¹*5¹+2¹*5²+2¹*5³=

2¹*(5⁰+5¹+5²+5³)

2²*5⁰+2²*5¹+2²*5²+2²*5³=

2²*(5⁰+5¹+5²+5³)

2³*5⁰+2³*5¹+2³*5²+2³*5³=

2³*(5⁰+5¹+5²+5³)

所以所有的质因数之和可以表示为：

(2⁰+2¹+2²+2³)*(5⁰+5¹+5²+5³)=

15*156=2340

---

也可以通过编译运行程序验证：

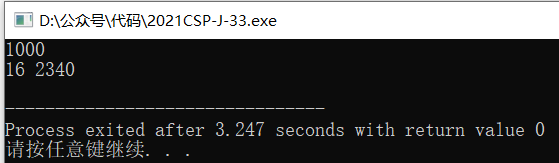
输入1000，输出为16 2340

所以本题的正确答案应该选择C。

真题解析34

(1)（Josephus 问题）有 n 个人围成一个圈，依次标号 0 至 n-1。从 0 号开始，依次 0, 1, 0, 1, … 交替报数，报到 1 的人会离开，直至圈中只剩下一个人。求最后剩下人的编号。

试补全模拟程序。

34. ①处应填（  ）A. i < n

B. c < n

C. i < n – 1

D. c < n – 1

解析：

背景知识：

约瑟夫问题：一个计算机科学和数学中的问题，在计算机编程的算法中，类似问题又称为约瑟夫环。

Josephus 问题来历：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

结构化程序设计（structured programming）：“面向结构”的程序设计方法即结构化程序设计方法， 是“面向过程”方法的改进， 结构上将软件系统划分为若干功能模块， 各模块按要求单独编程， 再由各模块连接， 组合构成相应的软件系统。该方法强调程序的结构性，思路清晰， 做法规范。结构化程序设计的三种基本结构是:顺序结构、分支结构和循环结构。

知识点分类：

C++程序设计-结构化程序设计-顺序结构、分支结构、循环结构

答案解析：

首先分析下题目所给的代码：

从代码分析可以看出，①处代码应该是控制循环程序什么时候停止。

根据题目要求，交替报数直至圈中只剩下一个人。

而c表示退出游戏的人数，n表示参加游戏的人数。

当c<n-1时，while循环正常进行；

当c=n-1时，圈内只剩1个人，退出循环。

所以本题的正确答案应该选择D。

35. ②处应填（  ）

A. i % 2 == 0

B. i % 2 == 1

C. p

D. !p

解析：

背景知识：

Josephus 问题来历：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

位运算：

任何信息在计算机中都是采用二进制表示的，数据在计算机中是以补码形式存储的，位运算就是直接对整数在内存中的二进制位进行运算。根据NOI大纲要求，入门级阶段需要掌握的位运算有与（&）、或（|）、非（~）、异或（^）、左移（<<）和右移(>>)。

知识点分类：

C++程序设计-结构化程序设计-顺序结构、分支结构、循环结构

答案解析：

首先分析下题目所给的代码：（如上）

从代码分析可以看出，②处代码应该是判断报数的人报了0还是1，报1的人要出圈离开游戏。

变量p表示参加游戏的人报的数字，值在0和1之间反复，初始值为0；

当p=0时，16行-19行if语句为假，当前编号的人不出圈。

当p=1时，16行-19行if语句为真，当前编号的人出圈。

---

选项A 表示只要编号为偶数的人都出圈，不符合题意

选项B 表示只要编号为奇数的人都出圈，不符合题意

选项C p的值为0

选项D !p中的”!”表示位运算中的非运算，所以!p的值为1

而题干中明确说明第一个人报数为0，报到 1 的人会离开，因此第一个人是不出圈的，所以②处应该填p。

本题的正确答案应该选择C。

36. ③处应填（   ）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1

解析：

背景知识：

Josephus 问题来历：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

自增自减运算符：在C++等高级程序设计语言中，自增或自减运算符的作用是在运算结束前（前置自增自减运算符）或运算结束后（后置自增自减运算符）将变量的值加（或减）1。例如：

++i    先使i的值自增1，再使用i的值

– – i   先使i的值自减1，再使用i的值

i++    使用i的值之后，使i的值自增1

i- –    使用i的值之后，使i的值自减1

知识点分类：

C++程序设计-基本运算-变量自增与自减运算

答案解析：

首先分析下题目所给的代码：（如上）

从代码分析和上一题的分析可以看出，当p=1，16行-19行if语句为真时，当前编号的人出圈，③处的代码应该是记录出圈的人数。而出圈的人数在程序中是使用变量c来表示，有一个人出圈，c的值就应该加1，所以本处应该填c++。

本题的正确答案应该选择C。

37. ④处应填（  ）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1

解析：

背景知识：

Josephus 问题来历：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

位运算：

任何信息在计算机中都是采用二进制表示的，数据在计算机中是以补码形式存储的，位运算就是直接对整数在内存中的二进制位进行运算。根据NOI大纲要求，入门级阶段需要掌握的位运算有与（&）、或（|）、非（~）、异或（^）、左移（<<）和右移(>>)。

运算规则如下：

与（&）

两个位都为1时，结果才为1

或（|）  

两个位都为0时，结果才为0

非（~） 

0变1，1变0

异或（^）

两个位相同为0，相异为1

左移（<<)

各二进位全部左移若干位，高位丢弃，低位补0

右移  (>>)

各二进位全部右移若干位

对无符号数，高位补0

对有符号数，有的补符号位，有的补0

知识点分类：

C++程序设计-基本运算-位运算

答案解析：

首先分析下题目所给的代码：（如上）

从之前题目的分析可知：

变量p表示参加游戏的人报的数字，值在0和1之间反复，初始值为0；

当p=0时，16行-19行if语句为假，当前编号的人不出圈。

当p=1时，16行-19行if语句为真，当前编号的人出圈。

题目中要求从 0 号开始，依次 0, 1, 0, 1, … 交替报数，通过对代码分析可知，④处的代码实现的功能是: 无论当前编号的人是否出圈，都要继续报数，直到循环结束。所以这里要让p的值在0和1之间交替出现，根据背景知识的介绍，我们可以使用异或运算来实现这个效果：

p ^=1 相当于 p = p ^ 1

当p=0时，p ^ 1= 0 ^ 1=1

当p=1时，p ^ 1= 1 ^ 1=0

由上边的计算可知，异或运算使得p的值在0和1之间交替反复。

所以本题的正确答案应该选择D。

38. ⑤处应填（  ）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1

解析：

背景知识：

Josephus 问题来历：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

求余：一种数学计算方法，是在整数运算中求一个整数x 除以另一个整数y的余数的运算，且不考虑运算的商。也称为模运算，“模”是“Mod”的音译，模运算多应用于程序编写中，运算符为%，Mod的含义即为求余。

知识点分类：

数学-数及其运算-数的概念，算数运算（加、减、乘、除、求余）

答案解析：

首先分析下题目所给的代码：（如上）

通过对代码分析可知，⑤处的代码实现的功能是: 改变i的值，因为题目要求是依次 0, 1, 0, 1, … 交替报数，所以报数的人一直在改变，变量i表示参加游戏的人的编号，如果不改变，每次就都是同一个人在报数了。根据背景知识的介绍，我们可以使用模运算来实现这个效果。

题目描述有 n 个人围成一个圈，依次标号 0 至 n-1。

所以i的取值范围是大于等于0，小于等于n-1。

C和D选项都无法改变变量i的值，所以可以首先排除；

对于A 选项 i++ , 我们可以假设现在i=n-1,那么i进行自增运算后就等于n，超出了给定的范围，所以也不正确。

最后来看B选项： i = (i + 1) % n

当i=0时，i=(i + 1) % n = 0

当i=1时，i=(i + 1) % n = 1

…

当i=n-2时，i=(i + 1) % n = n-1

当i=n-1时，i=(i + 1) % n = 0

可以看出i的值在0到n-1之间反复，符合题目要求。

所以本题的正确答案应该选择B。

真题解析39

(2)（矩形计数）平面上有n个关键点，求有多少个四条边都和x轴或者y轴平行的矩形，满足四个顶点都是关键点。给出的关键点可能有重复，但完全重合的矩形只计一次。试补全枚举算法。

39. ①处应填（   ）

A. a.x != b.x ? a.x < b.x : a.id < b.id

B. a.x != b.x ? a.x < b.x : a.y < b.y

C. equals(a,b) ? a.id < b.id : a.x < b.x

D. equals(a,b) ? a.id < b.id : (a.x != b.x ? a.x < b.x : a.y < b.y)

解析：

背景知识：

三目运算符：三目运算符又称为“三元运算符”和“条件运算符”，在java、C、C++、python、JavaScript、PHP等编程语言中都有三目运算符。三目运算符的作用就是判断，可以理解为if条件判断的简化版。

三目运算符语法：

布尔表达式？表达式1：表达式2

运算过程：

如果布尔表达式的值为真 ，则返回 表达式1的值

如果布尔表达式的值为假 ，则返回 表达式2的值

知识点分类：

C++程序设计-基本运算-三目运算

答案解析：

首先分析下题目所给的代码：

根据对代码分析可知，整段程序的计算步骤为：

1.坐标输入

2.坐标排序

3.坐标去重

4.枚举坐标

5.输出答案

在第二步坐标排序的sort函数代码中可以发现，坐标值有交换的操作，每次比较相邻的值，应该是冒泡排序。排序操作要能二分出特定的坐标，这里需要比较x和y的值才能完成。

①处是完善cmp函数：

选项A和选项C没有考虑比较坐标y的值，可以排除。

选项B和选项D都可以比较坐标x，y的值，选项D还会比较下标编号id。而cmp函数只能比较坐标，不能比较下标，所以可以排除选项D。

本题的正确答案应该选择B。

40. ②处应填（ ）

A. i == 0 || cmp(A[i], A[i – 1])

B. t == 0 || equals(A[i], A[t – 1])

C. i == 0 || !cmp(A[i], A[i – 1])

D. t == 0 || !equals(A[i], A[t – 1])

解析：

背景知识：

运算符：一种告诉编译器执行特定的数学或逻辑操作的符号。C++ 常用的运算符类型有：

• 算术运算符
• 关系运算符
• 逻辑运算符
• 位运算符
• 赋值运算符
• 杂项运算符

逻辑运算符：将两个或多个关系表达式连接成一个或使表达式的逻辑反转

&& 称为逻辑与运算符：

将两个表达式连接成一个。两个表达式必须都为 true，整个表达式才为 true。

||  称为逻辑或运算符：

如果两个操作数中有任意一个 true，则条件为 true。

! 称为逻辑非运算符：

反转一个表达式的逻辑状态。使一个表达式从 true 变成了 false，或者从 false 变成了 true。

知识点分类：

C++程序设计-基本运算-逻辑运算：与（&&）、或（||）、非（!）

答案解析：

首先分析下题目所给的代码：（如上）

根据对代码分析可知，整段程序的计算步骤为：

1.坐标输入

2.坐标排序

3.坐标去重

4.枚举坐标

5.输出答案

在第三步坐标去重的 unique函数代码中可以发现，具体去重方法是：如果去重数组中没有存储内容，或者最后加入的坐标与当前坐标不一致，就进行去重操作。

②处是完善unique去重函数，根据上边的分析可以确定此处一定是使用equals函数判断前后坐标是否一致，而不是使用cmp函数对坐标进行比较。所以可以排除选项A和选项C。

同时我们通过对unique函数的代码分析可知，当加入坐标与当前坐标不一致也就是不相等时进行去重操作，而equals函数是判断两个坐标是否相等的，所以可以排除选项B。

选项D中：

t == 0 

表示去重数组中没有存储内容

!equals(A[i], A[t – 1])

表示加入的坐标与当前坐标不相等

||  逻辑或运算符  表示前后两个条件满足一个即可

所以本题的正确答案应该选择D。

41、③处应填（  ）

A. b – (b – a) / 2 + 1

B. (a + b + 1) » 1

C. (a + b) » 1

D. a + (b – a + 1) / 2

解析：

背景知识：

位运算：任何信息在计算机中都是采用二进制表示的，数据在计算机中是以补码形式存储的，位运算就是直接对整数在内存中的二进制位进行运算。根据NOI大纲要求，入门级阶段需要掌握的位运算有与（&）、或（|）、非（~）、异或（^）、左移（<<）和右移(>>)。

位运算规则：

与（&）：两个位都为1时，结果才为1

或（|）： 两个位都为0时，结果才为0

非（~）：  0变1，1变0

异或（^）：两个位相同为0，相异为1

左移（<<）: 各二进位全部左移若干位，高位丢弃，低位补0
右移（>>）：各二进位全部右移若干位，对无符号数，高位补0，有符号数，各编译器处理方法不一样，有的补符号位（算术右移），有的补0（逻辑右移）

二分法：英语称为binary search，也称折半搜索。是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始：

1. 如果中间元素正好是要查找的元素，则搜索过程结束；

2. 如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较；

3. 如果在某一步骤数组为空，则代表找不到。

知识点分类：

C++程序设计-基本运算-位运算

算法-基础算法-二分法

答案解析：

首先分析下题目所给的代码：（如上）

根据对代码分析可知，整段程序的计算步骤为：

1.坐标输入

2.坐标排序

3.坐标去重

4.枚举坐标

5.输出答案

③处是完善binary_search二分查找函数，变量a和变量b表示二分查找的左右 边界，根据二分查找算法的原理可以判断mid变量是变量a和变量b的中点，即mid=(a+b)/2，根据背景知识中位运算的介绍我们可知：(a+b)/2=(a+b)>>1

所以本题的正确答案应该选择C。

42. ④处应填（  ）

A. !cmp(A[mid], p)

B. cmp(A[mid], p)

C. cmp(p, A[mid])

D. !cmp(p, A[mid])

解析：

背景知识：

逻辑运算符：将两个或多个关系表达式连接成一个或使表达式的逻辑反转

&& 称为逻辑与运算符：

将两个表达式连接成一个。两个表达式必须都为 true，整个表达式才为 true。

||  称为逻辑或运算符：

如果两个操作数中有任意一个 true，则条件为 true。

! 称为逻辑非运算符：

反转一个表达式的逻辑状态。使一个表达式从 true 变成了 false，或者从 false 变成了 true。

二分法：英语称为binary search，也称折半搜索。是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始：

1. 如果中间元素正好是要查找的元素，则搜索过程结束；

2. 如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较；

3. 如果在某一步骤数组为空，则代表找不到。

知识点分类：

算法-基础算法-二分法

答案解析：

首先分析下题目所给的代码：（如上）

根据对代码分析可知，整段程序的计算步骤为：

1.坐标输入

2.坐标排序

3.坐标去重

4.枚举坐标

5.输出答案

④处仍然是完善binary_search二分查找函数，通过对代码分析可知，满足此处的条件时，mid要加1，也就是当p的值比A[mid]的值大时更新二分查找的左边界。

所以本题的正确答案应该选择B。

43. ⑤处应填（ ）

A. A[i].x == A[j].x

B. A[i].id < A[j].id

C. A[i].x == A[j].x && A[i].id < A[j].id

D. A[i].x < A[j].x && A[i].y < A[j].y

解析：

背景知识：

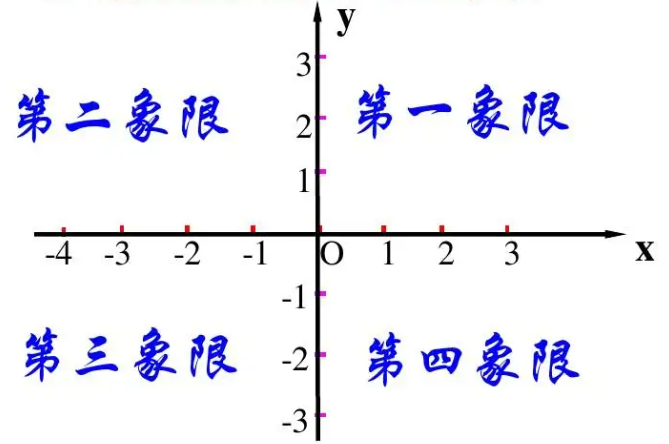
平面直角坐标系：在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称为直角坐标系。直角坐标系有两个坐标轴，其中横轴为x轴，取向右的方向为正；纵轴为y轴，取向上的方向为正。直角坐标系所在的平面称为坐标平面。两条坐标轴将坐标平面分为四个区域，分别称为第一、二、三、四象限，如下图所示：

逻辑运算符：将两个或多个关系表达式连接成一个或使表达式的逻辑反转

&& 称为逻辑与运算符：

将两个表达式连接成一个。两个表达式必须都为 true，整个表达式才为 true。

||  称为逻辑或运算符：

如果两个操作数中有任意一个 true，则条件为 true。

! 称为逻辑非运算符：

反转一个表达式的逻辑状态。使一个表达式从 true 变成了 false，或者从 false 变成了 true。

知识点分类：

数学-初中数学-初中平面几何

答案解析：

首先分析下题目所给的代码：（如上）

根据对代码分析可知，整段程序的计算步骤为：

1.坐标输入

2.坐标排序

3.坐标去重

4.枚举坐标

5.输出答案

⑤处要实现的功能是枚举矩形左下角与右上角坐标，然后查看另一条对角线上的两个角是否存在。通过背景知识中对平面直角坐标系的介绍可知，本题中讨论的矩形均处于第一象限，矩形左下角点的x,y坐标值都小于矩形右上角的x,y坐标值，此处应该使用：A[i].x < A[j].x && A[i].y < A[j].y

所以本题的正确答案应该选择D。