《实践 创新 — 计算机的普及要从娃娃做起》关于举办2023年江苏省"信息与未来"小学生编程C++









第一题:
题目大意:给定一个区间 [a, b],求区间内满足奇数位和等于偶数位和的数字个数。解题思路:遍历区间内的每一个数字,计算其奇数位和与偶数位和,若相等则计数器加一。最 后输出计数器的值即可。具体实现如下:1. 初始化计数器 count 为 0。2. 遍历区间内的每一个数字 i,对于每个数字,初始化奇数位和 odd_sum 和偶数位和 even_sum 为 0。3. 将数字 i 转换为字符串 s,方便按位访问。4. 遍历字符串 s 的每一位,若当前位数为奇数,则将其加到 odd_sum 中,否则加到 even_sum 中。5. 遍历结束后,若 odd_sum 等于 even_sum,则计数器 count 加一。6. 遍历区间内所有数字后,输出计数器 count 的值。
以下是完整的代码实现:
#include <iostream>
#include <string>
using namespace std;int main() {
int a,b;
cin>>a>>b;
int count=0;
for(int i=a;i<=b;++i) {
string s=to_string(i);
int odd_sum=0,even_sum=0;
for(int j=0; j<s.size();++j){
if(j%2==0) {
odd_sum+=s[j]-'0';
}
else{
even_sum +=s[j]-'0';
}
}
if(odd_sum==even_sum) {
++count;
}
}
cout<<count<<endl;
return 0;
}
第二题:
这道题目的关键在于将输入的字符串转换为整数,然后计算两个时刻之间的百分之一秒数。我 们可以先将输入的字符串按照冒号和小数点进行分割,然后将时、分、秒、百分之一秒分别转 换为整数。接下来,我们可以将两个时刻转换为总的百分之一秒数,然后计算它们之间的差值 即可。
具体实现如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int a,b,c,d,e,f,g,h;
scanf("%d:%d:%d.%d",&a,&b,&c,&d);
scanf("%d:%d:%d.%d",&e,&f,&g,&h);
int aa,bb;
aa=a*360000+b*6000+c*100+d;
bb=e*360000+f*6000+g*100+h;
cout<<bb-aa;
}
第三题:
本题的目标是找到两张图像经过平移后,重叠部分的像素数量尽可能多。我们可以通过枚举所 有可能的平移方式,计算重叠部分的像素数量,然后取最大值。具体实现过程如下:1. 读取两张图像的尺寸和像素值。2. 初始化最大重叠像素数量为 0。3. 枚举所有可能的平移方式,包括上下左右平移。对于每一种平移方式,计算重叠部分的 像素数量。4. 如果当前平移方式的重叠像素数量大于最大重叠像素数量,则更新最大重叠像素数量。5. 输出最大重叠像素数量。
#include<iostream>
#include<vector>
using namespace std;
int main(){
int n1,m1,n2,m2;
cin>>n1>>m1;
vector<vector<int>> img1(n1,vector<int>(m1));
for(int i=0;i<n1;++i){
for(int j=0;j<m1;++j){
cin>>img1[i][j];
}
}
cin>>n2>>m2;
vector<vector<int>> img2(n2,vector<int>(m2));
for(int i=0;i<n2;++i){
for(int j=0;j<m2;++j){
cin>>img2[i][j];
}
}
int max_overlap=0;
for(int dx=-n1;dx<n2;++dx){
for(int dy=-m1;dy<m2;++dy){
int overlap=0,non_overlap=0;
for(int i=0;i<n1;++i){
for(int j=0;j<m1;++j){
int x=i+dx;
int y=j+dy;
if(x>=0 && x<n2 && y>=0 && y<m2){
if(img1[i][j]==img2[x][y]){
++overlap;
}
else{
++non_overlap;
}
}
}
}
if(non_overlap==0){
max_overlap=max(max_overlap,overlap);
}
}
}
cout<<max_overlap<<endl;
return 0;
}
通过这种枚举平移方式的方法,我们可以找到使得重叠部分像素数量最大的平移方式,并输出 最大重叠像素数量。
第四题:
思路 1:语义分析
如果不考虑输入/输出语句,我们可以把任何程序都理解成一个函数 f,f(x, y, z, …) 计算从程 序 “初始状态” 到 “结束状态” 时所有变量 x, y, z, … 的值。任何 X 语言的程序都可以看成是这样 的函数。由于语句的特殊性,一个重要而且有趣的观察是任何一段 X 语言的程序,都可以改写成如下 等价的形式:
if(L1<=x && x<=R1) {
y=C1;
}
if(L2<=x && x<=R2) {
y=C2;
}
...
其中条件范围 [L , R ], [L , R ], … 互不相交且覆盖所有可能的 x 的范围——也就是说,一段 X 语言的程序的本质是把 x 的值划分成若干区间,并为每个区间赋一个 y 的值。例如:
if(x>10){
if(x>100){
y=1;
if(x<1000) {
y=99;
y=2;
}
}
}
可以改写成
if(INT_MIN<=x && x<=100){
y=y;
// 继承之前的数值
}
if(101<=x && x<=999){
y=2;
}
if(1000<=x && x<=INT_MAX) {
y=1;
}
我们可以称这种形式为 “简单” 的程序。那么,对于任何一个 “不那么简单” 的程序:
if(x>C){
// “简单” 的程序
}
我们总是把它重新改写成简单的程序——因此我们只要递归地改写,最终就能把任何程序改写 成 “简单” 的程序,从而得到可能的 y 的数值。这个思路在程序分析领域相当于直接求解程序 的 “语义”,但这里有一些细节需要小心处理,例如顺序执行语句,后者的结果会覆盖前者。
思路 2:边界值分析
另一个思路是我们可以解释执行程序,将一个具体的 x 值代入程序,就可以得到一个 y 的数 值。解释执行程序可以看成是表达式求值——如果我们把条件的 true/false 代入表达式,if (true) { P } 和 if (false) { P } 的 “值” 就相当显然了。但解释执行有一个缺点:x 可以是所有 int 范围内的整数,因此枚举的代价很大。但同时,我 们也观察到,对于许多 x 数值,程序的路径都是重复的,最终得到 y 的结果也是相同的,例如:
if(x>9999){
if(x<10000001){
y=1;
}
}
对于上面的程序,对于任意的 10, 000 ≤ x ≤ 10, 000, 000,都会走入 y = 1 的路径——枚举这些 x 是明显的浪费。因此,我们只需要考虑 “导致条件变化” 的 x 数值——对于任意比较的常数 c,我们代入 c − 1, c, c + 1 即可触发所有与之相关的条件路径。在软件领域,这个技术被称为 “boundary value analysis”,即边界值分析。使用这个思路能大幅简化代码的实现。
代码实现看起来我们需要解析一个类似 C++ 语法的程序;但因为程序中有足够多的空格,因此我们完 全可以使用 cin 首先读入一个字符串,然后根据字符串来解析后续的输入:
cin>>token;
if(token=="if") {
// 必定是四个字符串:"(x" "运算符" "常数)" "{"
}
if(token=="y") {
// 必定是两个字符串:"=" "常数;"
}
if(token=="}") {
// 本⾏结束
}
将代码解析成内存中的数据结构后,就可以使用递归实现求解,或是用栈来处理配对的 { 和 }。
第五题:⽂本压缩
编码与数据压缩
首先,我们观察到,压缩字符串能够使用比原串更多的字母表。我们不妨考虑更 “简单” 的压 缩问题,允许使用 “ABCD” 四个额外字母压缩 01 字符串。那么我们可以建立如下规则:
那么,我们就可以实现接近 1/2 的压缩比:
00 -> A 01 -> B 10 -> C 11 -> D 0 -> 0 1 -> 1
010101101101000
B B B C D B A0
把小写字母字符串想象成是 26 进制数,大小写字母和数字字符串想象成是 26 × 2 + 10 = 62 进制数。我们实际上可以实现一个 “进制转换”,以实现数据的压缩。在实际实现时,观察到
这意味着我们可以用 4 位 62 进制数表示 5 位 26 进制数——来实现 4/5 的压缩比。对于实际的压缩软件例如 zip 和 rar,它们都是二进制文件——一个字节的 256 种情况都可以用来编码。
利⽤ “英⽂⽂本” 的特征
然而这种 “进制转换” 的编码方式完全没有利用输入数据的特殊性——对于英文单词,许多单词 甚至是句子是存在重复的——“onceuponatime” 就在样例数据中出现了十多次。如果我们用 “A” 替代它,并且在文件的头部标记 “Aonceuponatime”,就可以减少数十的长度。实际上,我们可以用上 A0, A1, A2, … B0, … ZZ 这些小写字母以外的字符编码那些 “高频” 的字 符串:这个过程可以迭代实现,固定一个长度 k 从频次最高的 k 长度字符串开始,依次分配字 符编码——编码后的字符还可以再次编码。同学们可以通过适当尝试,达到预期的压缩比。
实际的中的压缩算法
实际中的压缩算法除了利用上述两个思路之外,还有更多的方法,但对解决这个问题不是必须 的:
2. 游程编码(Run-Length Encoding,RLE):这种方法适用于具有大量重复字符的文本。在 游 程 编 码 中 , 连 续 重 复 的 字 符 被 替 换 为 该 字 符 及 其 重 复 次 数 。例 如 , 字 符 串“AAAABBBCCDAA”将被编码为“4A3B2C1D2A”。解压缩时,只需将计数与字符相乘, 还原为原始字符串。
3. Lempel-Ziv-Welch(LZW)算法:这是一种基于字典的压缩方法。在压缩过程中,算法会 构建一个字典,其中包含输入文本中的字符和字符串。然后,原始文本中的字符串被替 换为字典中相应条目的索引。解压缩时,可以使用相同的字典将索引转换回原始字符 串。
4. Burrows-Wheeler Transform(BWT):这种方法通过重新排列文本中的字符,使得具有 相似上下文的字符靠近在一起,从而提高其他压缩算法的效果。BWT并不直接压缩数 据,而是作为其他压缩算法(如游程编码或霍夫曼编码)的预处理步骤。解压缩时,需要对数据进行逆变换,以恢复原始文本。
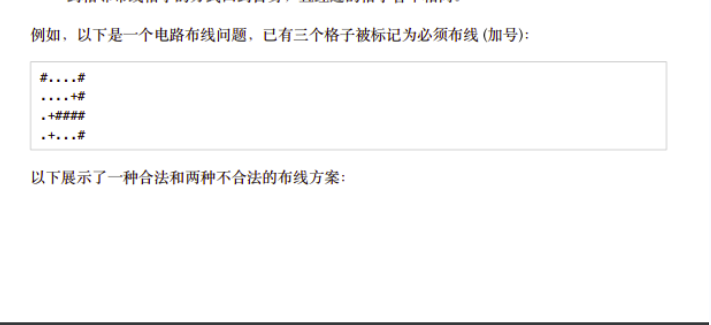
第六题:电路布线
枚举法求解
如果我们为每一个可布线的格子 “.” 枚举是否布线,我们就得到了一个判定问题:判定某个具 体的布线是否满足连通和无回路的要求:对于连通性,我们可以从任意 “+” 开始,使用深度优先/宽度优先搜索/迭代,找出所有可 达的加号。可达加号的数量必须和第一个连通块的数量一致。对于无回路,我们可以检查连通块中的边数是否等于点数减一。我们也可以遍历所有的边,并插入并查集数据结构来判定连通性和无回路。连通性和回路的判定是非常基础的教科书算法问题。
算法优化
对于 6 × 6 的方格,至少有一个已布线的方格,我们需要检查 种不同的方案。我们可以通 过两种方式进行剪枝:如果当前的解存在无法连通的方格或已经存在回路,则应剪枝。如果当前的解无论如何都无法成为最优解,则应剪枝。我们需要为剩余部分的解估算一 个下界,例如剩下的方格总数。这种方法称为分支定界 (branch and bound);增加适当的搜索优化,可以通过大部分到全部测试用例。一个有趣的思路是可以把电路分成上下两部分分别枚举,上半部分和下半部分枚举的数量都不 超过 = 262, 144。我们考虑上半部分的两种方案:
方案 1:
...++. ####++
方案 2:
+++++. ####++
毫无疑问,方案 2 是比方案 1 更 “好” 的——从下半部分看来,它们的 “接缝” 是完全一致的,但 方案 2 布了更多的线。因此,我们可以分别对上半部分和下半部分进行剪枝——对于同一种 “接 缝形状” 和连通性,我们只要保留布线数量最多的方案即可。在实际实现中,我们只需要排除 掉存在孤岛的不合法方案,即可通过所有测试用例。