一、 单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项)
1 在Linux系统终端中,以下那个命令用于创建一个新的目录( )
A newdir
B mkdir
C create
D mkfold
答案 B
2 由0,1,2,3,4中选取4个数字,能组成( )个不同四位数注:最小的四位数是1000最大的四位数是9999)
A 96
B 18
C 120
D 84
答案 A
3 假设n 是图的顶点的个数,m 是图的边的个数,为求解某一问题有下面四种不同时间复杂度的算法
对于m=O(n)的稀疏图而言下面的四个选项,哪一项的渐近时间复杂度最小
A O(m*sqrt(logn)*loglogn)
B O(n^2+m)
C O(n^2/logm+mlogn)
D O(m+nlogn)
答案 A
4 假设有n 根柱子,需要按照以下规则依次放置编号为1、2、3、…的圆环:每根柱子的底部固定,顶部可以放入圆环,每次从柱子顶部放入圆环时,需要保证任何两个相邻圆环的编号之和是一个完全平方数。请计算当有4根柱子时,最多可以放置( )个圆环
A 7
B 9
C 11
D 5
答案 C
5 以下对数据结构的表述不恰当的一项是
A 队列是一种先进先出(FIFO)的线性结构
B 哈夫曼树的构造过程主要是为了实现图的深度优先搜索
C 散列表是一种通过散列函数将关键字映射到存储位置的数据结构
D 二又树是一种每个结点最多有两个子结点的树结构
答案 B
6 以下连通无向图中,( )一定可以用不超过两种颜色进行染色
A 完全三叉树
B 平面图
C 边双连通图
D 欧拉图
答案 A
7 最长公共子序列长度常常用来衡量两个序列的相似度。其定义如下:给定两个序列X=
{x1,x2,x3,…xm}和Y={y1,y2,y3…yn},最长公共子序列(LCS)问题的目标是找到一个最长的新序
列Z= {z1,z2,z3…zk},使得序列 既是序列X 的子序列,又是序列Y的子序列,且序列Z的长度k 在
满足上述条件的序列里是最大的。(注:序列A 是序列B 的子序列,当且仅当在保持序列B 元素顺序的
情况下,从序列B中删除若千个元素,可以使得剩余的元素构成序列A。测序列“ABCAAAABA”和“ABABCBABA”的最长公共子序列长度为( )
A 4
B 5
C 6
D 7
答案 C
8 一位玩家正在玩一个特殊的掷骰子的游戏,游戏要求连续掷两次骰子,收益规则如下:玩家第一次掷
出x点,得到2x元;第二次掷出y点,当y=x 时玩家会失去之前得到的2x元而当y!=x时玩家能保住第一
次获得的2x元。上述x,y∈[1,2,3,4,5,6]。 例如:玩家第一次掷出3点得到6元后,但第二次再次掷出3
点,会失去之前得到的6元,玩家最终收益为0元:如果玩家第一次掷出3点第二次掷出4点,则最终
收益是6元。假设骰子挑出任意一点的概率均为1/6,玩家连续掷两次般子后所有可能情形下收益的平
均值是多少?
A 7
B 35/6
C 16/3
D 19/3
答案 B
9 假设我们有以下的C++代码:
inta=5,b=3,c=4;
bool res= a&b||c^b && a|c
提示:在 C++中,逻辑运算的优先级从高到低依次为: 逻辑非(!)逻辑与(&&)、逻辑或(||)。位运算的
优先级从高到低依次为: 位非(~)、位与(&)、位异或(^)、位或(|)。同时,双目位运算的优先级高于双
目逻辑运算:逻辑非和位非优先级相同,且高于所有双目运算符
A true
B false
C 1
D 0
答案 A
10 假设快速排序算法的输入是一个长度为n的已排序数组,且该快速排序算法在分治过程总是选择第1个元素作为基准元素。以下哪个选项描述的是在这种情况下的快速排序行为?
A 快速排序对于此类输入的表现最好因为数组已经排序
B 快速排序对于此类输入的时间复杂度是O(nlogn)。
C 快速排序对于此类输入的时间复杂度是O(n^2)
D 快速排序无法对此类数组进行排序因为数组已经排序
答案 C
11 以下哪个命令,能将一个名为“main.cpp”的 C++源文件,编译并生成一个名为”main“的可执行文件? ( )
A g++ -o main main.cpp
B g++ -o main.cpp main
C g++ main -o main.cpp
D g++ main.cpp -o main.cpp
**答案 A **
12 在图论中,树的重心是树上的一个结点,以该结点为根时,使得其所有的子树中结点数最多的子树的结点数最少。一棵树可能有多个重心。请问下面哪种树一定只有一个重心( )
A 4个结点的树
B 6个结点的树
C 7个结点的树
D 8个结点的树
答案 C
13 如图是一张包含6个顶点的有向图,但顶点间不存在拓扑序。如果要删除其中一条边,使这6个顶点能进行拓扑排序,请问总共有多少条边可以作为候选的被删除边?
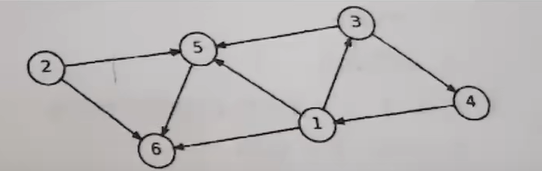
A 1
B 2
C 3
D 4
答案 C
14

A 10
B 11
C 12
D 13
答案 B
15 现在用如下代码来计算x^n,其时间复杂度为( )
double quick_power(double x,unsigned int n){
if (n==0) return 1;
if (n==1) return x;
return quick_power(x,n/2)*quick_power(x,n/2)*((n&1)?x:1);
}
A O(n)
B O(1)
C O(logn)
D O(nlogn)
答案 A
二、 阅读程序(程序输入不超过数组成字符串定义的范围:判断题正确填√,错误填×;除特殊说明外,判断题1.5分,选择题3分,共计40分)
1
01 #incTude <iostream>
02 using namespace std;
03
04 unsigned short f(unsigned short x) {
05 x ^=x << 6;
06 x ^=x >> 8;
07 return x;
08 }
09
10 int main() {
11 unsigned short x;
12 cin >> x;
13 unsigned short y = f(x);
14 cout << y << end1;
15 return 0;
16 }
假设输入的x是不超过65535的自然数,完成下面的判断题和单选题
判断题
16 当输入非零时,输出一定不为零( )
答案 T
17 将f函数的输入参数的类型改为unsigned int,程序的输出不变( )
答案 F
18 当输入为“65535”时,输出为“63”( )
答案 T
19 当输入为“1”时,输山为“64”。
答案 F
单选题
20 当输入为“512”时,输出为()
A “33280” B “33410” C “33106” D “33346″
答案 B
21 当输入为“64”时,执行完第5行后x的值为()
A “8256” B “4130” C “4128” D “4160“
答案 D
2
01 #include <iostream>
02 #include <cmath>
03 #include <vector>
04 #include <algorithm>
05 using namespace std;
06
07 long long solvel(int n) {
08 vector<boo1> p(n+1,true);
09 vector<long long> f(n+1,0),g(n+1,0);
10 f[1] = 1;
11 for (int i= 2;i*i<= n; i++) {
12 if (p[i]) {
13 vector<int> d;
14 for (int k=i;k <= n; k *= i) d.push_back(k);
15 reverse(d.begin(),d.end());
16 for (int k :d){
17 for (int j= k;j<= n;j+= k) {
18 if (p[j]){
19 p[j] = false;
20 f[j] = i;
21 g[j] = k;
22 }
23 }
24 }
25 }
26 }
27 for (int i= sqrt(n) + 1;i<= n;i++){
28 if (p[i]){
29 f[i] = i;
30 g[i] = i;
31 }
32 }
33 long long sum = 1;
34 for (int i=2;i<= n;i++){
35 f[i]=f[i / g[i]]*(g[i]*f[i]-1) / (f[i]-1);
36 sum += f[i];
37 }
38 return sum;
39 }
40
41 long long solve2(int n){
42 long 1ong sum = 0;
43 for (int i= 1;i <= n; i++) {
44 sum +=i*(n /i);
45 }
46 return sum;
47 }
48
49 int main() {
50 int n;
51 cin >>n;
52 cout << solvel(n)<< endl;
53 cout << solve2(n)<< endl;
54 return 0;
55 }
判断题
22 将第15 行删去,输出不变( )
答案 F
23 当输入为“10”时,输出的第一行大于第二行。( )
答案 F
24 当输入为“1000”时,输出的第一行与第二行相等( )
答案 T
单选题
25 solve1(n)的时间复杂度为( )

答案 D
26 solve2(n)的时间复杂度为( )
A O(n^2)B O(n) C O(nlogn) D O(nsqrt(n))
答案 B
27 输入为”5”时,输出的第二行为( )
A 20 B 21 C 22 D 23
答案 B
3
01 #include <vector>
02 #include <algorithm>
03 #include <iostream>
04
05 using namespace std;
06
07 boo1 f0(vector<int>& a, int m,int k) {
08 int s = 0;
09 for (int i=0,j=0;i< a.size();i++) {
10 while (a[i]- a[j]> m) j++;
11 s+= i-j;
12 }
13 return s >= k;
14 }
15
16 int f(vector<int>& a,int k) {
17 sort(a.begin(),a.end());
18
19 int g = 0;
20 int h = a.back()- a[0];
21 while (g <h){
22 intm=g+(h-g)/2;
23 if(f0(a,m,k)){
24 h=m;
25 }else {
26 g=m+1;
27 }
28 }
29
30 return g;
31 }
32
33 int main() {
34 int n, k;
35 cin >> n>> k;
36 vector<int> a(n,0);
37 for (int i=0;i<n;i++) {
38 cin >>a[i];
39 }
40 cout << f(a,k) << end1;
41 return 0;
42 }
判断题
28 将第24行的“m”改为“m-1”,输出有可能不变,而剩下情况为少1。( )
答案 T
29 将第22行的“g +(h-g)/2改为“(h+g)>>1”,输出不变。( )
答案 T
30 当输入为“5 7 2 -4 5 1 -3”,输出为”5”。( )
答案 T
单选题
31 设a数组中最大值减最小值加1为A,则f函数的时间复杂度为( )

答案 C
32 将第10行中的”>”替换为”>=”,那么原输出与现输出的大小关系为( )
A 一定小于 B 一定小于等于且不一定小于 C 一定大于等于且不一定大于 D 以上三种情况都不对
答案 B
33 当输入为“5 8 2 -5 3 8 -1 2”时,输出为( )
A "13" B "14" C "8" D "15"
答案 B
三、完善程序(单选题,每小题3分,共计 3 分)
1第k小路径
给定一张n个点 m 条边的有向无环图,顶点编号从0到n-1。对于一条路径,我们定义“路径序列”为该路径从起点出发依次经过的顶点编号构成的序列。求所有至少包含一个点的简单路径中,“路径序列”字典序第k小的路径。保证存在至少 k条路径,上述参数满足1<=n,m<=10^5 和1<=k<=10^18表示 .在程序中,我们求出从每个点出发的路径数量。超过10^18的数都用 10^18表示。然后我们根据k的值和每个顶点的路径数量,确定路径的起点,然后可以类似地依次求出路径中的每个点。
试补全程序。
01 #include <iostream>
02 #include<algorithm>
03 #incTude <vector>
04
05 const int MAXN = 100000;
06 const long long LIM =10000000000000000001l
07
08 int n,m,deg[MAXN];
09 std::vector<int> E[MAXN];
10 long 1ong k,f[MAXN];
11
12 int next(std::vector<int> cand, 1ong long &k) {
13 std::sort(cand.begin0,cand.end());
14 for (int u : cand) {
15 if ( ① ) return u;
16 k -= f[u];
17 }
18 return -1;
19 }
20
21 int main() {
22 std::cin >>n>> m >> k;
23 for (int i=0;i<m; ++i){
24 int u, v;
25 std::cin >> u>> v;
26 E[u].push_back(v);
27 ++deg[v];
28 }
29 std::vector<int> Q;
30 for (int i= 0;i<n; ++i)
31 if (!deg[i]) Q.push_back(i);
32 for (int i=0;i<n;++i){
33 int u= Q[i];
34 for (int v :E[u]){
35 if ( ② ) Q.push_back(v);
36 –deg[v];
37 }
38 }
39 std::reverse(Q.begin(),Q.end());
40 for (int u:Q){
41 f[u] = 1;
42 for (int v : E[u]) f[u] = ③
43 }
44 int u= next(Q,k);
45 std::cout << u << std::endl;
46 while ( ④ ) {
47 ⑤;
48 u= next(E[u],k);
49 std::cout << u << std::end1;
50 }
51 return 0;
52 }
34 ①处应该填写( )
A k>=f[u] B k<=f[u] C k>f[u] D k<f[u]
答案 B
35 ②处应该填写( )
A deg[v]==1 B deg[v]==0 C deg[v]>1 D deg[v]>0
答案 A
36 ③处应该填写( )
A std::min(f[u]+f[v],LIM)
B std::min(f[u]+f[v]+1,LIM)
C std::min(f[u]*f[v],LIM)
D std::min(f[u]*(f[v]+1),LIM)
答案 A
37 ④处应该填写( )
A u!=1 B !E[u].empty() C k>0 D k>1
答案 D
38 ⑤处应该填写( )
A k+=f[u] B k-=f[u] C --k D ++k
答案 C
2 最大值之和
给定整数序列 a0…an-1,求该序列所有非空连续子序列的最大值之和。上述参数满足1<=n<=10^5 和 1<=ai<=10^8
一个序列的非空连续子序列可以用两个下标l和r(其中0 <=l<=r<=n)表示,对应的序列为al,al+1,…ar。两个非空连续子序列不同,当且仅当下标不同
例如,当原序列为[1,2,1,2] 时,要计算子序列[1]、[2]、[1]、[2]、[1,2]、[2,1]、[1,2]、[1,2,1]、[2,1,2]、[1,2,1,2] 的最大值之和,答案为 18。注意[1,1]和[2,2] 虽然是原序列的子序列,但不是连续子序列,所以不应该被计算。另外,注意其中有一些值相同的子序列,但由于他们在原序列中的下标不同,属于不同的非空连续子序列,所以会被分别计算.解决该问题有许多算法,以下程序使用分治算法时间复杂度 O(nlogn)。
试补全程序
01 #include <iostream>
02 #include<algorithm>
03 #include <vector>
04
05 const int MAXN = 100000;
06
07 int n;
08 int a[MAXN];
09 long 1ong ans;
10
11 void solve(int l, int r) [
12 if(l+1==r){
13 ans += a[l];
14 return;
15 }
16 int mid=(l+r)>>1;
17 std::vector<int> pre(a + mid,a+r);
18 for (int i=l;i<r-mid; ++i) ①
19 std::vector<long long> sum(r – mid + 1);
20 for (int i=0;i<r-mid;++i) sum[i+1]= sum[i]+ pre[i];
21 for (int i=mid-1,j=mid,max = 0;i>= l;–i){
22 while (j<r&& ② ) ++j;
23 max = std::max(max,a[i]);
24 ans += ③;
25 ans += ④ ;
26 }
27 solve(l,mid);
28 solve(mid,r);
29 }
30
31 int main(){
32 std::cin >> n;
33 for (int i=0;i<n;++i) std::cin >> a[i];
34 ⑤
35 std::cout << ans << std::end1;
36 return 0;
37 }
39 ①处应填( )
A pre[i]= std::max(pre[i - 1],a[i - 1])
B pre[i + 1]= std::max(pre[il,pre[i+ 1])
C pre[i]=std::max(pre[i - 1],a[i])
D pre[i]= std::max(pre[i],pre[i - 1])
答案 D
40 ②处应填( )
A a[j]< max
B a[j]< a[i]
C pre[j - mid]< max
D pre[j - mid] > max
答案 B
41 ③处应填( )
A (long long)(j - mid)* max
B (long long)(j - mid) * (i - l)* max
C sum[j - mid]
D sum[j - mid]*(i- l)
答案 A
42 ④处应填( )
A (long long)(r -j)* max
B (long long)(r -j)*i*(mid -i)*max
C sum[r - mid] - sum[j - mid]
D (sum[r - mid] - sum[j - mid])* (mid - i)
答案 C
43⑤处应填( )
A solve(0,n) B solve(0,n - 1)
C solve(1,1) D solve(1,n - 1)
答案 A